音程(インターバル)
音程とは、ふたつの音と音の高さの隔たりのことです。
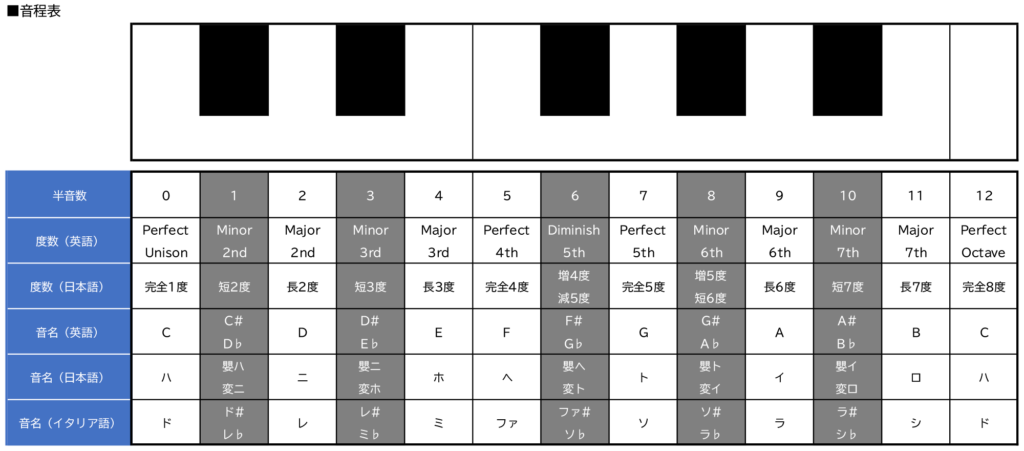
音程の表し方として一般的に用いられているのは「半音」と「全音(半音ふたつ分)」に基づく西洋の方法で、単位は「度」。ただ、コード表記と密接な関係があるので覚えるなら英語読みをオススメします。
同じ音を1度として、ピアノでいう白鍵(幹音)がひとつ上がるにつれ数字がひとつ増えます。1、4、5、8度は「Perfect(完全)」、それ以外は「Major(長)」がつきます。
Majorに対して半音下がる(ピアノでいう黒鍵部分)と「Minor(短)」がつきますが、Perfect 5th(完全5度)の半音下のみ「Diminish(減)」となります。
ちなみに4度と5度に対しては半音上を言うことがあり、この場合は「Augment(増)」がつきます。
1、4、5、8度がなぜ「Perfect(完全)」なのかというと、音の響きの相性がいいからです。詳しくは音律の項目を参照してください。
倍音
音の高さは振動数、つまり周波数によって決まります。ただ、基本となる周波数の音に対し、実際はその2倍3倍という整数倍の周波数がプラスで鳴っています。この音を倍音と言います。
例えば64HzのC(ド)の音を鳴らしたとします。この周波数には128Hz、256Hz、512Hz、1024Hz…という周波数も含まれて鳴っています。実際に弦やピアノでCの音を鳴らし続けていると高いCの音が聴こえてくると思いますが、これが倍音です。

この倍音が音楽に影響する例として、例えば2つの音を同時に鳴らしたとします。すると、それぞれの音の倍音も同時に鳴っていることになるので、それぞれの倍音によっては音にうねりが生じ、響きを邪魔することがあります。これは音律の影響もあるので、詳しくは以下の音律の項目を参照してください。
音律
オクターブ間の音(周波数比1:2の音程)を相対的にどのような間隔で鳴らすかを規定したものが音律です。そしてある楽器を特定の音律に調整することを調律(チューニング)と言います。いくつか種類がありますが、現在の音楽ではほぼ平均律が使用されています。
①ピタゴラス音律
「三平方の定理」で有名なピタゴラスが作った音律です。
例えば1本の弦があったとして、1/2(中央)の部分を押さえて弾くとPerfect Octave(完全8度、オクターブ上)の音が鳴ります。周波数比1:2です。
同様に、弦の1/3の部分を押さえて長い方を弾くとPerfect 5th(完全5度、CでいうG)の音が鳴ります。周波数比3:2です。
ピタゴラスは、基本波とこの3倍波を同時に聞くと協和していて心地よい、ということを発見し、この3倍音と2と3という素数を用い、12音からなる「ピタゴラス音律」を作りました。
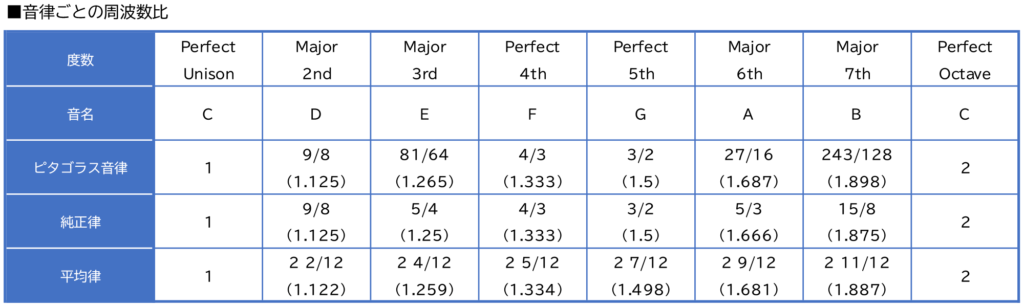
ただ、この音律はPerfect 4thとPerfect 5thの音はきれいに響きますが、Major 3rdの音は周波数比が1:81になるので単純な整数比にならず、きれいに響きません。Major 6thの音も同様の理由できれいに響きません。
西洋音楽で用いられていたこのピタゴラス音律ですが、Major 3rdやMajor 6thがよく使われるようになった15世紀あたりから使われなくなったと言われています。
②純正律
純正律は周波数比が単純な整数比でできているので、音と音が混ざり合っても倍音のうねりが発生しない、つまり純粋な響きの和音になります。これにより、ピタゴラス音律の欠点であったMajor 3rdやMajor 6thの響きを解決しています。
ただ純正律にも欠点があり、主音が変わると周波数比が異なるという現象が起きます。
例えばCを基準として調律した純正律で、主音をCとした時のPerfect 5th、Gの周波数比は3:2(1.5)ですが、主音をDとした時のPerfect 5th、Aの周波数比は40:27(1.481)となり、比率が異なります。
つまり、隣り合う音と音の比が等しくないため、転調ができないということになります。
③平均律
平均律は転調ができないという純正律の欠点を補うため、オクターブを均等な周波数比で12分割した音律です。
これにより、隣り合う音と音の比が等しくなるので調和を保ちながらの転調が可能となります。
ただし、平均律は純正律の響きを美しくすることを犠牲にしているので、ユニゾンと各オクターブ間以外の和音は必ずうなりが発生します。これは1オクターブを12の音で割り切ることができないのが理由です。
なので平均律は純正律のようなきれいな調和は生み出せません。
ちなみに1オクターブを1200等分した「セント」という単位もよく使われます。平均律でいう半音が100セントとなります。
半音より狭い音程は「微分音」と言い、微分音は理論上無限に存在はしますが、全音(200セント)を何分割するかによって3分音、4分音というような呼び方もし、インド音楽やジプシー音楽でしばしば見受けられます。